Unser Goldener Schnitt Rechner ermöglicht es Ihnen, die harmonischen Proportionen nach dem Goldenen Schnitt einfach und schnell zu berechnen. Egal, ob Sie die längere Strecke, die kürzere Strecke oder die Gesamtlänge haben – unser Tool liefert Ihnen sofort die Ergebnisse.
Goldener Schnitt Rechner
So funktioniert der Goldener Schnitt Rechner
Der Goldener Schnitt Rechner arbeitet mit der mathematischen Konstante φ (Phi), die den Wert von etwa 1,618 hat. Diese Konstante repräsentiert das Verhältnis, das als Goldener Schnitt bekannt ist. Sie geben eine der drei möglichen Eingaben an: die längere Strecke, die kürzere Strecke oder die Gesamtlänge.
Basierend auf dieser Eingabe berechnet der Rechner die beiden fehlenden Werte unter Anwendung der Beziehung des Goldenen Schnitts. Der Rechner zeigt nicht nur die Ergebnisse, sondern auch den vollständigen Rechenweg, sodass Sie den Prozess nachvollziehen können.
Die Bedienung des Rechners ist einfach: Wählen Sie die Strecke, die Sie eingeben möchten, und füllen Sie das entsprechende Feld aus. Der Rechner sperrt automatisch die anderen Felder, um sicherzustellen, dass keine fehlerhaften Berechnungen stattfinden.
Anschließend klicken Sie auf „Berechnen“, und die Ergebnisse werden sofort angezeigt. Falls Sie Ihre Eingaben ändern möchten, können Sie auf „Zurücksetzen“ klicken, um alle Felder zu leeren und eine neue Berechnung durchzuführen.
Goldenen Schnitt berechnen: Formel und Erklärung
Die Berechnung des Goldenen Schnitts basiert auf der einzigartigen mathematischen Beziehung zwischen den Strecken.
Diese Beziehung wird durch die Formel:
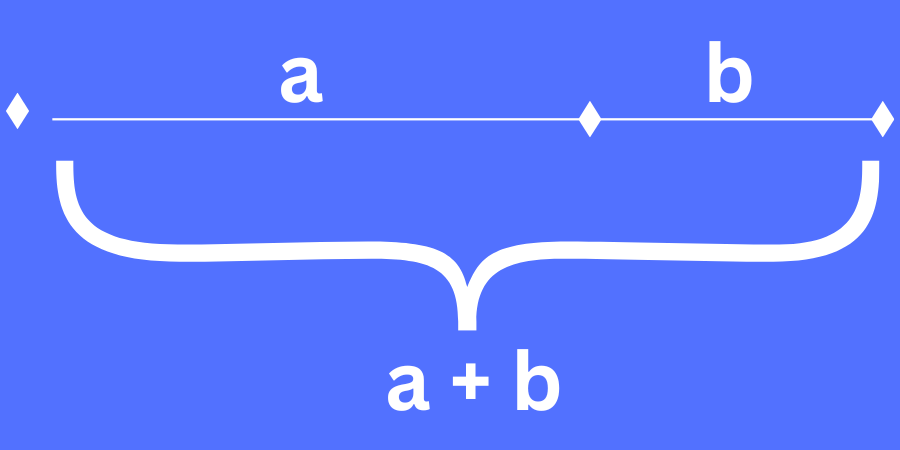
\(\frac{a}{b} = \frac{a + b}{a} = \phi\)dargestellt, wobei a die längere Strecke und b die kürzere Strecke ist. Diese Formel sagt aus, dass das Verhältnis der längeren Strecke zur kürzeren Strecke dasselbe ist wie das Verhältnis der Gesamtlänge (a + b) zur längeren Strecke. Diese Proportionen führen zu einer harmonischen Teilung, die in der Natur, Kunst und Architektur häufig vorkommt.
Um die Formel zu veranschaulichen, nehmen wir an, dass Sie die Gesamtlänge (a + b) kennen und den Wert von a berechnen möchten.
Die Formel für a lautet dann:
\(a = \frac{(a + b)}{\phi}\)Für b ergibt sich:
\(b = a \times \frac{1}{\phi}\)Mit diesen Formeln können Sie jede beliebige Strecke berechnen, solange Sie einen der drei Werte kennen.
Anwendungsgebiete und Einsatzmöglichkeiten
Der Goldene Schnitt findet in zahlreichen Bereichen Anwendung, darunter Kunst, Architektur, Grafikdesign, Fotografie und sogar Naturwissenschaften. In der Kunst wird der Goldene Schnitt oft verwendet, um Gemälde oder Skulpturen zu gestalten, die als besonders harmonisch empfunden werden. Künstler wie Leonardo da Vinci und Salvador Dalí haben in ihren Werken häufig den Goldenen Schnitt verwendet, um Proportionen zu schaffen, die das Auge angenehm empfindet.
In der Architektur wird der Goldene Schnitt genutzt, um Gebäude und Räume zu entwerfen, die ästhetisch ausgewogen sind. Klassische Beispiele hierfür sind die Pyramiden von Gizeh oder der Parthenon in Athen, bei denen das Verhältnis von Höhe zu Basis dem Goldenen Schnitt entspricht.
Im Grafikdesign und der Fotografie wird der Goldene Schnitt verwendet, um Layouts und Kompositionen zu erstellen, die visuell ansprechend sind. Fotografen nutzen die Regel des Goldenen Schnitts, um Bildausschnitte zu wählen, die das Auge des Betrachters führen und das Bild harmonisch erscheinen lassen.
Auch in der Naturwissenschaft wird das Prinzip des Goldenen Schnitts in der Untersuchung von Wachstumsprozessen und natürlichen Strukturen wie Schneckenhäusern, Sonnenblumen und DNA-Molekülen beobachtet.
Mathematischer Hintergrund des Goldenen Schnitts
Der Goldene Schnitt ist nicht nur ein künstlerisches Konzept, sondern auch ein tiefes mathematisches Prinzip.
Er wird als die positive Lösung der quadratischen Gleichung definiert:
\(x^2 – x – 1 = 0\)Die positive Lösung dieser Gleichung ergibt die Zahl φ (Phi), die ungefähr 1,618 beträgt. Diese Zahl taucht in der Fibonacci-Folge auf, einer Reihe von Zahlen, bei der jede Zahl die Summe der beiden vorhergehenden ist (1, 1, 2, 3, 5, 8, 13, …). Interessanterweise nähert sich das Verhältnis aufeinanderfolgender Fibonacci-Zahlen zunehmend dem Wert von φ an, je weiter man in der Folge fortschreitet.
Der Goldene Schnitt hat auch eine enge Beziehung zur Geometrie. Ein Beispiel ist das sogenannte Goldene Rechteck, ein Rechteck, dessen Seitenlängen im Verhältnis des Goldenen Schnitts stehen. Wenn man ein Quadrat von diesem Rechteck abschneidet, bleibt ein weiteres, kleineres Rechteck übrig, das ebenfalls das Verhältnis des Goldenen Schnitts aufweist.
Dieser Prozess kann theoretisch unendlich fortgesetzt werden, was zu der sogenannten Goldenen Spirale führt, die sich in der Natur häufig findet.
Geschichte und kulturelle Bedeutung des Goldenen Schnitts
Der Begriff „Goldener Schnitt“ stammt aus der Renaissance, wurde jedoch bereits in der Antike untersucht. Der griechische Mathematiker Euklid beschrieb das Prinzip in seinem Werk „Die Elemente“. Während der Renaissance gewann der Goldene Schnitt als idealer Proportionsstandard in der Kunst und Architektur an Popularität.
Der Mathematiker und Künstler Luca Pacioli nannte den Goldenen Schnitt „Divina Proportione“ und arbeitete eng mit Leonardo da Vinci zusammen, der den Goldenen Schnitt in seinen berühmten Werken wie dem „Vitruvianischen Menschen“ verwendete.
Im Laufe der Geschichte haben sich viele Denker und Künstler mit dem Goldenen Schnitt beschäftigt. In der modernen Kultur taucht der Goldene Schnitt in Designprinzipien, Markenlogos und sogar Musikkompositionen auf. Trotz seiner antiken Ursprünge bleibt der Goldene Schnitt ein aktuelles Thema in der Kunst, Mathematik und Naturwissenschaft.
Weitere Mathe-Rechner:
