Dieser Volumenrechner hilft Ihnen, das Volumen verschiedener geometrischer Formen zu berechnen. Wählen Sie einfach die gewünschte Form aus, geben Sie die erforderlichen Maße ein und klicken Sie auf „Volumen berechnen“. Das Tool bietet Ihnen eine schnelle und einfache Möglichkeit, präzise Volumenberechnungen durchzuführen.
Volumenrechner
Wählen Sie eine geometrische Form und füllen Sie die Felder aus, um das Volumen zu berechnen:

Quader Volumen berechnen: Formel & Erklärung
Ein Quader ist ein dreidimensionales Rechteck mit sechs rechteckigen Flächen.
Das Volumen eines Quaders wird berechnet, indem man die Länge, Breite und Höhe miteinander multipliziert.

Die Formel zur Berechnung des Volumens eines Quaders lautet:
\( \text{Volumen} = \text{Länge} \times \text{Breite} \times \text{Höhe} \)
Würfel Volumen berechnen: Formel & Erklärung
Ein Würfel ist ein spezieller Quader, bei dem alle Seiten gleich lang sind.
Um das Volumen eines Würfels zu ermitteln, wird die Kantenlänge dreimal mit sich selbst multipliziert.
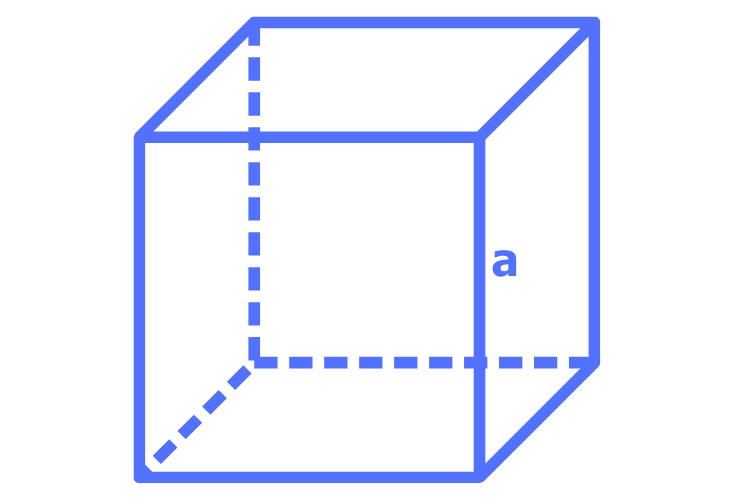
Die Formel zur Berechnung des Volumens eines Würfels lautet:
\( \text{Volumen} = a^3 \), wobei \(a\) die Kantenlänge ist.
Kugel Volumen berechnen
Eine Kugel ist eine perfekte dreidimensionale Form, bei der alle Punkte auf der Oberfläche denselben Abstand zum Mittelpunkt haben.
Das Volumen einer Kugel wird mit einer speziellen Formel berechnet, die den Radius der Kugel verwendet.
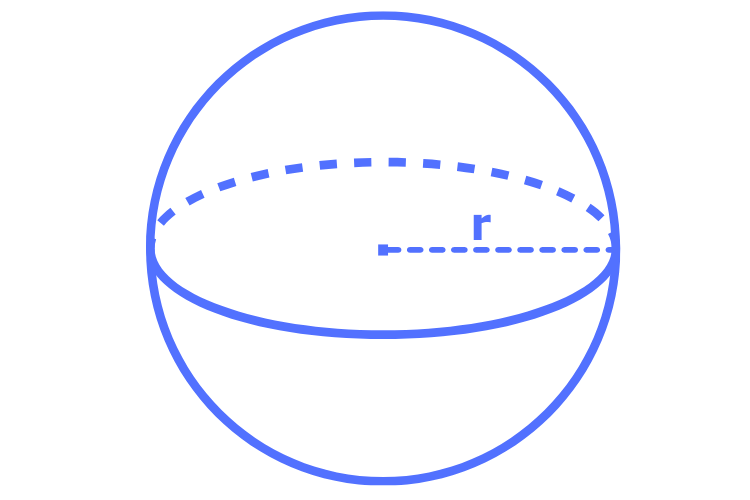
Die Formel zur Berechnung des Volumens einer Kugel lautet:
\( \text{Volumen} = \frac{4}{3} \pi r^3 \), wobei \(r\) der Radius der Kugel ist.
Halbkugel Volumen berechnen
Eine Halbkugel ist die Hälfte einer Kugel. Um das Volumen einer Halbkugel zu berechnen, wird die Formel für das Kugelvolumen durch zwei geteilt.
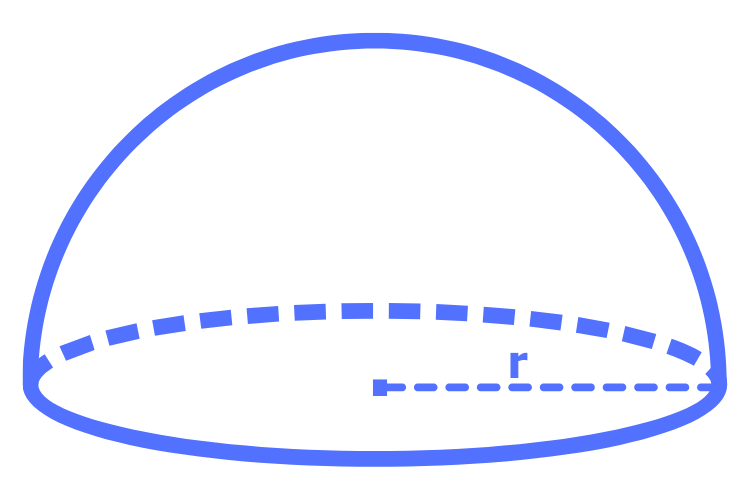
Die Formel zur Berechnung des Volumens einer Halbkugel lautet:
\( \text{Volumen} = \frac{2}{3} \pi r^3 \), wobei \(r\) der Radius der Halbkugel ist.
Zylinder Volumen berechnen
Ein Zylinder ist eine dreidimensionale Form mit zwei parallelen, identischen kreisförmigen Basen.
Das Volumen eines Zylinders wird berechnet, indem man die Fläche der Basis mit der Höhe des Zylinders multipliziert.
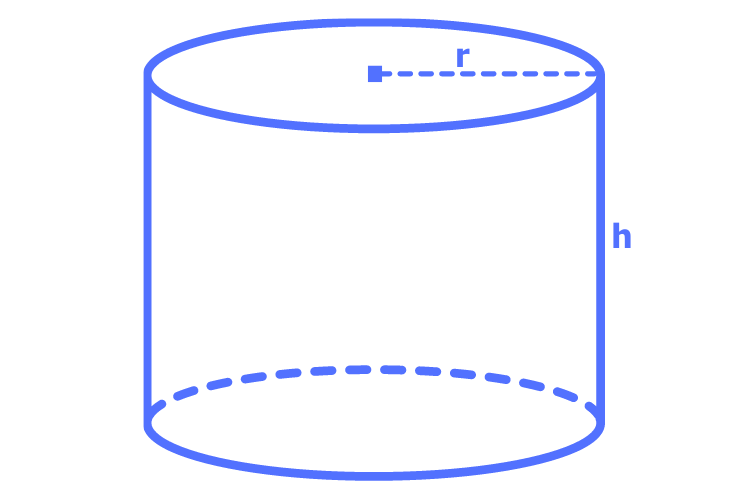
Die Formel zur Berechnung des Volumens eines Zylinders lautet:
\( \text{Volumen} = \pi r^2 h \), wobei \(r\) der Radius der Basis und \(h\) die Höhe ist.
Kegel Volumen berechnen
Ein Kegel ist eine dreidimensionale Form mit einer kreisförmigen Basis, die sich zu einem Punkt verjüngt.
Das Volumen eines Kegels wird berechnet, indem man das Volumen eines Zylinders mit derselben Basis und Höhe durch drei teilt.
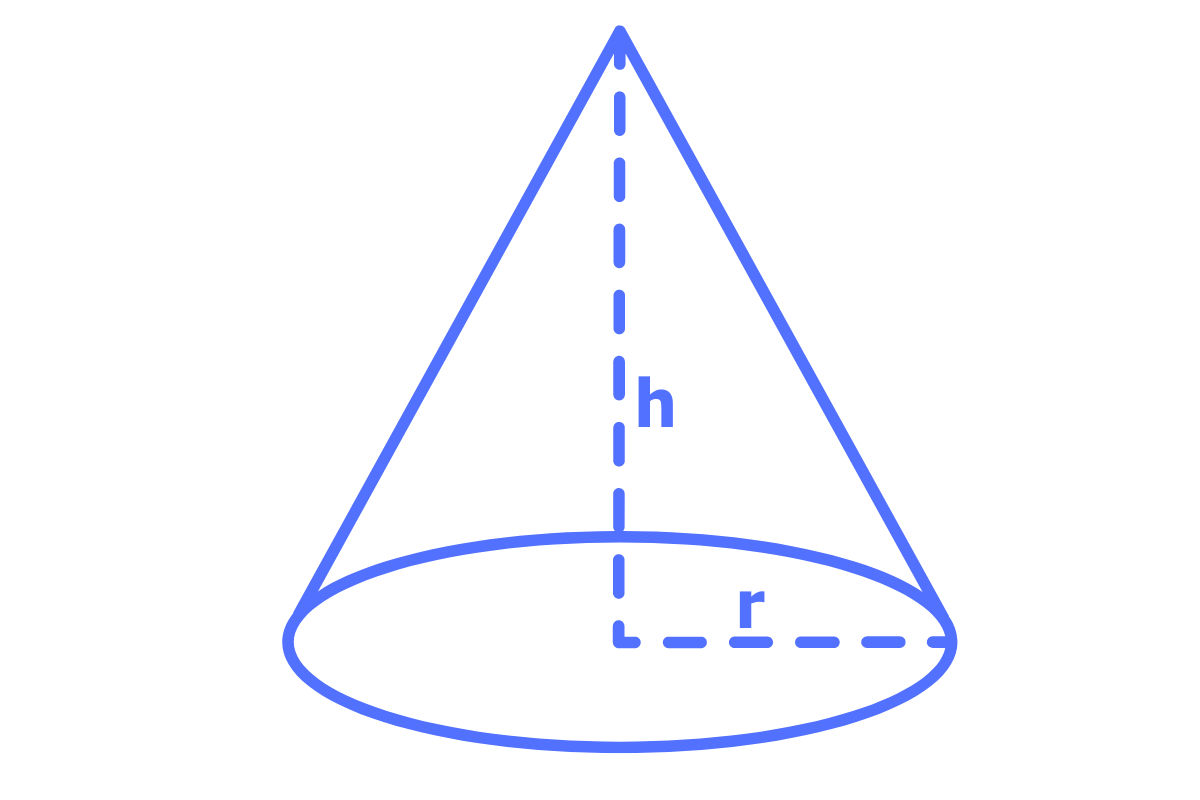
Die Formel zur Berechnung des Volumens eines Kegels lautet:
\( \text{Volumen} = \frac{1}{3} \pi r^2 h \), wobei \(r\) der Radius der Basis und \(h\) die Höhe ist.
Pyramide Volumen berechnen
Eine Pyramide ist eine dreidimensionale Form mit einer polygonalen Basis und dreieckigen Seiten, die zu einem Punkt zusammenlaufen.
Das Volumen einer Pyramide wird berechnet, indem man die Grundfläche mit der Höhe multipliziert und das Ergebnis durch drei teilt.
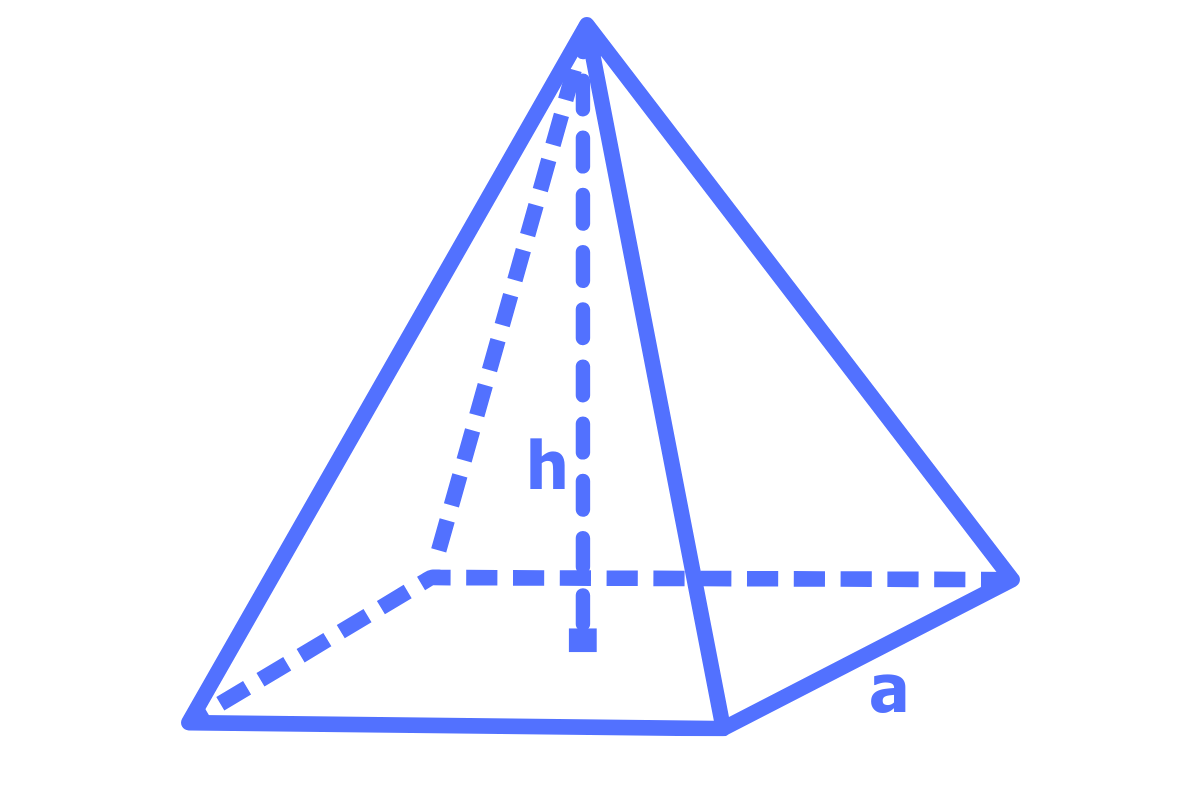
Die Formel zur Berechnung des Volumens einer Pyramide lautet:
\( \text{Volumen} = \frac{1}{3} \text{Grundfläche} \times \text{Höhe} \)
Ellipsoid Volumen berechnen
Ein Ellipsoid ist eine dreidimensionale Form, die wie eine gestreckte Kugel aussieht.
Es wird durch drei verschiedene Halbachsen beschrieben.
Das Volumen eines Ellipsoids wird mit einer speziellen Formel berechnet, die alle drei Halbachsen berücksichtigt.

Die Formel zur Berechnung des Volumens eines Ellipsoids lautet:
\( \text{Volumen} = \frac{4}{3} \pi abc \), wobei \(a\), \(b\), und \(c\) die Halbachsen sind.
Mehr Tools wie dieses:
- Kreis Rechner
- Würfel-Rechner
- Kubikmeter Rechner (m3)
- Quadratmeter Rechner (auch mit mehreren Flächen)
