Willkommen beim Logarithmus-Rechner! Dieses praktische Tool hilft Ihnen, logarithmische Berechnungen schnell und einfach durchzuführen. Geben Sie zwei der drei Werte (Basis, Numerus oder Logarithmuswert) ein, und der Rechner ermittelt automatisch den fehlenden Wert. Ideal für Studenten, Lehrer und alle, die mit Logarithmen arbeiten.

Logarithmus Rechner

Logarithmus Rechner

Gib Basis, Numerus oder Logarithmuswert ein (zwei Werte),
der fehlende Wert wird automatisch berechnet.

log =
Rundung auf 10 Nachkommastellen

Begriffsdefinition: Elemente der Logarithmusrechnung

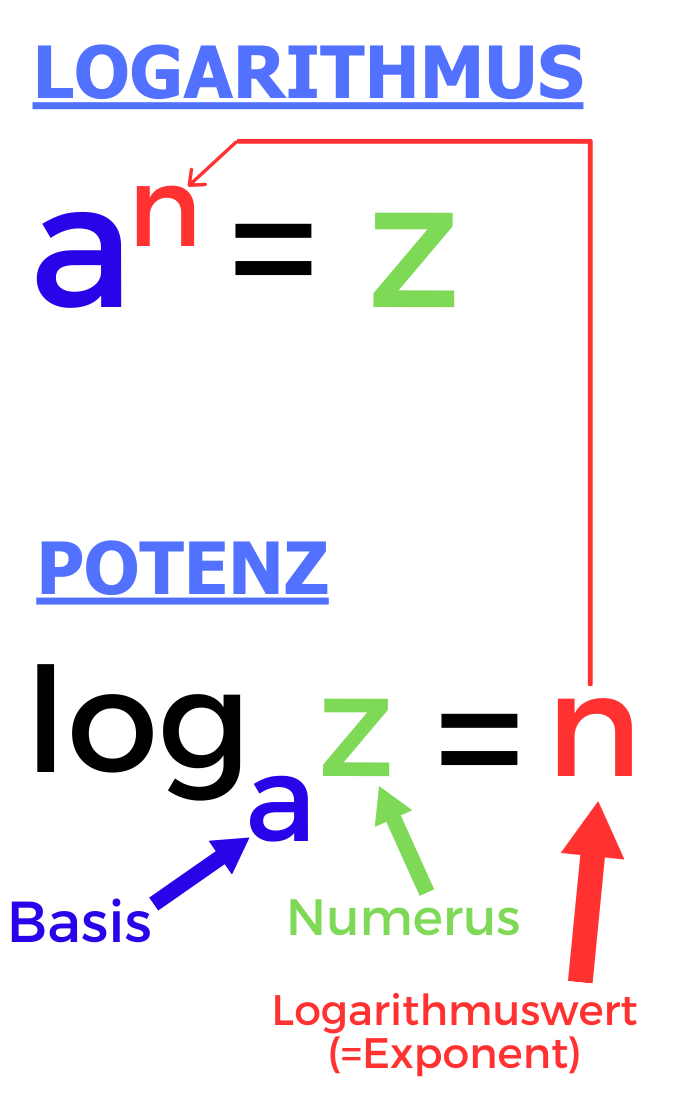
log (Logarithmus)

Der Logarithmus ist eine mathematische Operation, die die Umkehrfunktion zur Potenzierung darstellt.
In der Schreibweise loga(z) = n bedeutet dies: Zu welcher Potenz muss die Basis a erhoben werden,
um den Wert z zu erhalten?

a (Basis)

Die Basis ist die Grundzahl des Logarithmus. Sie bestimmt, auf welches Zahlensystem sich der Logarithmus bezieht.
Häufig verwendete Basen sind:

  • 10 (dekadischer Logarithmus, oft einfach als „log“ geschrieben)
  • e ≈ 2,71828… (natürlicher Logarithmus, oft als „ln“ geschrieben)
  • 2 (binärer Logarithmus, oft in der Informatik verwendet)

z (Numerus)

Der Numerus ist die Zahl, von der der Logarithmus berechnet wird. In der Gleichung loga(z) = n
ist z der Numerus. Es gilt immer: z = an.

n (Logarithmus oder Exponent)

Der Wert n ist das Ergebnis der Logarithmusoperation. Er gibt an, zu welcher Potenz die Basis a erhoben
werden muss, um den Numerus z zu erhalten. In der Gleichung an = z ist n der Exponent.

\( \text{Zusammengefasst gilt: Wenn } \log_a(z) = n, \text{ dann ist } a^n = z. \text{ } \)

Diese Beziehung bildet die Grundlage für alle Logarithmusberechnungen.


Wofür benötigt man Logarithmusrechnung?

Logarithmen spielen in vielen Bereichen von Wissenschaft und Alltag eine wichtige Rolle:

  1. Wissenschaft und Technik:
    • In der Akustik zur Messung von Schallpegeln (Dezibel-Skala)
    • In der Erdbebenkunde zur Darstellung der Richter-Skala
    • In der Chemie zur Berechnung des pH-Werts
  2. Finanzwesen:
    • Zur Berechnung von Zinseszins und Wachstumsraten
    • Bei der Analyse von Finanzmarkttrends
  3. Informatik und Datenverarbeitung:
    • Zur Analyse von Algorithmen und deren Laufzeitkomplexität
    • In der Datenkompression und Informationstheorie
  4. Naturwissenschaften:
    • In der Biologie zur Beschreibung von Wachstumsprozessen
    • In der Astronomie zur Darstellung von Helligkeitsskalen von Himmelskörpern
  5. Psychologie und Wahrnehmung:
    • Zur Beschreibung der menschlichen Wahrnehmung von Reizen (Weber-Fechner-Gesetz)
  6. Musik:
    • Zur Beschreibung von Tonintervallen und Frequenzverhältnissen
  7. Ingenieurwesen:
    • Bei der Analyse von Signalen und Systemen
    • In der Regelungstechnik

Logarithmen ermöglichen es, sehr große oder sehr kleine Zahlen kompakt darzustellen und Multiplikationen in einfachere Additionen umzuwandeln. Dies macht sie zu einem unverzichtbaren Werkzeug in vielen wissenschaftlichen und praktischen Anwendungen.

Weiter Tools: